
In einem Vibrating-Reed-Experiment werden die elastischen Materialeigenschaften über die Frequenz und die Dämpfung von Biegeeigenschwingungen von dünnen Plättchen gemessen. Die Bewegungsgleichung für eine solche Schwingung läßt sich nicht unmittelbar angeben, da die auftretenden Kräfte zunächst nicht bekannt sind.
Man betrachte ein dünnes Plättchen der Länge ![]() , Breite
, Breite ![]() und Dicke
und Dicke ![]() .
Bei einer Biegedeformation wird die konvexe Seite des Plättchens gedehnt, die
konkave gestaucht. Im Innern muß es eine neutrale Fläche geben, deren Länge
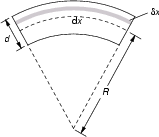
sich beim Biegen nicht ändert. Abb. 5.1 zeigt einen kleinen Ausschnitt
der Länge
.
Bei einer Biegedeformation wird die konvexe Seite des Plättchens gedehnt, die
konkave gestaucht. Im Innern muß es eine neutrale Fläche geben, deren Länge
sich beim Biegen nicht ändert. Abb. 5.1 zeigt einen kleinen Ausschnitt
der Länge ![]() des gebogenen Plättchens in Seitenansicht.
des gebogenen Plättchens in Seitenansicht.
|
Abb. 5.1: Seitenansicht eines kleinen Teils des gebogenen Plättchens.
|
Das schraffierte Teilstück im Abstand ![]() von der neutralen Fläche
erfährt eine Elongation um
von der neutralen Fläche
erfährt eine Elongation um ![]() . Die dabei auftretende Verzerrung
ist gegeben durch
. Die dabei auftretende Verzerrung
ist gegeben durch
![]() und wird
hervorgerufen von an der Stirnfläche
und wird
hervorgerufen von an der Stirnfläche ![]() angreifenden longitudinalen Kräften.
Für nicht zu große mechanische Spannungen
angreifenden longitudinalen Kräften.
Für nicht zu große mechanische Spannungen ![]() gilt dabei der
einfache lineare Zusammenhang
gilt dabei der
einfache lineare Zusammenhang
mit dem Youngschen Modul ![]() .
Die Kraft läßt sich in diesem Fall also schreiben als
.
Die Kraft läßt sich in diesem Fall also schreiben als
Natürlich werden die longitudinalen Kräfte oberhalb der neutralen Fläche
die Kräfte unterhalb dieser Fläche gerade kompensieren (sonst ergäbe sich eine
Beschleunigung in ![]() -Richtung), jedoch resultiert
aus der Gesamtheit der Kräfte ein Biegemoment
-Richtung), jedoch resultiert
aus der Gesamtheit der Kräfte ein Biegemoment
mit der sogenannten Biegesteifigkeit ![]() , die (natürlich nur für den Spezialfall
gänzlich rechteckiger Geometrie) durch
, die (natürlich nur für den Spezialfall
gänzlich rechteckiger Geometrie) durch ![]() gegeben ist.
gegeben ist.
Auf der gesamten Länge ![]() des Plättchens wird die Krümmung
natürlich nicht unbedingt konstant sein. Der Krümmungsradius kann
allgemein beschrieben werden durch den aus der Differentialgeometrie
bekannten analytischen Ausdruck
des Plättchens wird die Krümmung
natürlich nicht unbedingt konstant sein. Der Krümmungsradius kann
allgemein beschrieben werden durch den aus der Differentialgeometrie
bekannten analytischen Ausdruck
wobei ![]() die vertikale Auslenkung aus der Ruhelage ist.
Im Falle kleiner Auslenkungen gilt
die vertikale Auslenkung aus der Ruhelage ist.
Im Falle kleiner Auslenkungen gilt
![]() , so daß der
Zähler in Gl.
, so daß der
Zähler in Gl.![]() (5.4) in guter Näherung durch 1 ersetzt werden kann.
Somit läßt sich das Biegemoment einfach darstellen als
(5.4) in guter Näherung durch 1 ersetzt werden kann.
Somit läßt sich das Biegemoment einfach darstellen als
Im statischen Gleichgewicht wird die Summe aller an einem Teilstück der
Länge ![]() angreifenden Biegemomente verschwinden. Dies erlaubt die Berechnung
der wirksamen transversalen (oder Scher-) Kräfte, denn es muß gelten
(vgl. Abb. 5.2):
angreifenden Biegemomente verschwinden. Dies erlaubt die Berechnung
der wirksamen transversalen (oder Scher-) Kräfte, denn es muß gelten
(vgl. Abb. 5.2):
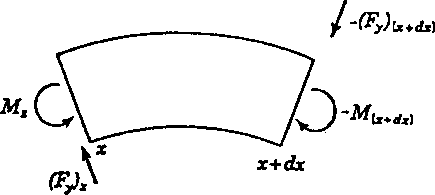
|
Abb. 5.2 Die am Teilstück der Länge |
Nach übergang zu infinitesimal kleinen Teilstücken ![]() kann man Biegemoment
und transversale Kraft approximieren durch
kann man Biegemoment
und transversale Kraft approximieren durch
sowie
Einsetzen dieser Ausdrücke in Gl.![]() (5.6) liefert unter Vernachlässigung
des in
(5.6) liefert unter Vernachlässigung
des in ![]() quadratischen Terms das einfache Ergebnis
quadratischen Terms das einfache Ergebnis
oder mit Gl.![]() (5.5)
(5.5)
Die auf das Teilstück der Länge ![]() wirkende Nettokraft
wirkende Nettokraft ![]() ist also
gegeben durch
ist also
gegeben durch
Diese Kraft beschleunigt die Masse
![]() des Segmentes
gemäß dem Newtonschen Gesetz:
des Segmentes
gemäß dem Newtonschen Gesetz:
Setzt man die Ausdrücke für ![]() und
und ![]() ein und definiert außerdem
ein und definiert außerdem

ergibt sich schließlich die gesuchte Bewegungsgleichung in der Form
Mit Hilfe des Separationsansatzes
(unterstrichene Größen sind komplexwertig, später wird als Lösung nur der
Realteil genommen)
läßt sich die partielle Differentialgleichung in zwei gewöhnliche aufspalten,
von denen die eine sofort durch
gelöst werden kann.
Für den ortsabhängigen Anteil erhält man die Gleichung
mit der Phasengeschwindigkeit
Man beachte, daß die so definierte Phasengeschwindigkeit frequenzabhängig ist.
Entsprechend ist die Wellenzahl
![]() nicht wie gewohnt proportional zur Frequenz, sondern zu deren Wurzel.
nicht wie gewohnt proportional zur Frequenz, sondern zu deren Wurzel.
Die Differentialgleichung (5.17) kann offensichtlich durch einen
Exponentialansatz gelöst werden. Als besonders geeignet zur Darstellung der
Lösung erweisen sich die Funktionen
die durch Differentiation ineinander übergehen. Die Lösungen haben dann die
Gestalt
mit reellen Konstanten
![]() , wobei im folgenden einfach
, wobei im folgenden einfach
![]() gesetzt wird.
Die übrigen vier Konstanten ergeben sich aus den Randbedingungen, denen das
Plättchen unterworfen ist. Der hier interessierende Fall ist derjenige, bei dem
das Plättchen an einem Ende (bei
gesetzt wird.
Die übrigen vier Konstanten ergeben sich aus den Randbedingungen, denen das
Plättchen unterworfen ist. Der hier interessierende Fall ist derjenige, bei dem
das Plättchen an einem Ende (bei ![]() ) fest eingespannt und am anderen Ende
(
) fest eingespannt und am anderen Ende
(![]() ) frei ist. Dort wirken dann keine Biegemomente und keine Kräfte
(Gln.
) frei ist. Dort wirken dann keine Biegemomente und keine Kräfte
(Gln.![]() (5.5), (5.10)), so daß die vier Randbedingungen lauten
(5.5), (5.10)), so daß die vier Randbedingungen lauten
Das Einsetzen dieser Bedingungen in (5.20) liefert nach einigen Umformungen die
Beziehung
deren Lösungen sich nur numerisch berechnen lassen. Die zu den erlaubten
![]() Werten gehörenden Eigenfrequenzen kann man darstellen als
Werten gehörenden Eigenfrequenzen kann man darstellen als
Die Modenkonstanten ![]() haben die Werte
haben die Werte
Die Frequenzen der Oberschwingungen sind also keine ganzzahligen Vielfachen der
Grundfrequenz; es gilt vielmehr
Als Lösung der Bewegungsgleichung (5.14) unter den Randbedingungen (5.21)
erhält man schließlich die Funktion
mit ![]() , der Maximalamplitude am freien Ende, und
der Wellenzahl der Eigenschwingungen
, der Maximalamplitude am freien Ende, und
der Wellenzahl der Eigenschwingungen
Die Verzerrungsamplituden für die verschiedenen Moden ergeben sich aus (5.26)
durch zweimaliges Differenzieren nach ![]() . Die Abbn. 5.3, 5.4 zeigen
(stark übertrieben) die Auslenkungs- und Verzerrungsamplituden für die ersten
vier Schwingungsmoden.
. Die Abbn. 5.3, 5.4 zeigen
(stark übertrieben) die Auslenkungs- und Verzerrungsamplituden für die ersten
vier Schwingungsmoden.
Bei einem Vibrating-Reed-Experiment kann man die Meßfrequenz offensichtlich
nicht frei wählen, sondern ist auf die Eigenfrequenzen des Plättchens
beschränkt. Im allgemeinen ist die Probendicke ![]() fest vorgegeben, so daß man
die Schwingungsfrequenz nur noch grob durch Wahl einer bestimmten Länge
fest vorgegeben, so daß man
die Schwingungsfrequenz nur noch grob durch Wahl einer bestimmten Länge ![]() einstellen kann.
einstellen kann.
Durch Einführen eines komplexen Youngschen Moduls
in der Schwingungsgleichung (5.14)
läßt sich auch die innere Dämpfung des Plättchens sehr einfach berücksichtigen.
Der sogenannte Verlustfaktor ![]() ist im Falle kleiner Dämpfung mit der
inneren Reibung
ist im Falle kleiner Dämpfung mit der
inneren Reibung ![]() identisch, die im Experiment gemessen wird /37/.
identisch, die im Experiment gemessen wird /37/.
Ein Lösungsansatz der Form
liegt nahe. ![]() kennzeichnet die Zeit bis zum Abklingen der
Schwingungsamplitude auf
kennzeichnet die Zeit bis zum Abklingen der
Schwingungsamplitude auf ![]() .
Einsetzen in die Bewegungsgleichung und Vergleich der Imaginärteile
führt auf die Beziehung
.
Einsetzen in die Bewegungsgleichung und Vergleich der Imaginärteile
führt auf die Beziehung
wobei ![]() angenommen wurde, so daß Gl.
angenommen wurde, so daß Gl.![]() (5.23) nach wie vor
Gültigkeit hat, die Verschiebung der Resonanzfrequenz durch die
Dämpfung also vernachlässigbar klein ist. Aus der Beobachtung des
Amplitudenzerfalls läßt sich somit die innere Reibung bestimmen (siehe auch
Kap.
(5.23) nach wie vor
Gültigkeit hat, die Verschiebung der Resonanzfrequenz durch die
Dämpfung also vernachlässigbar klein ist. Aus der Beobachtung des
Amplitudenzerfalls läßt sich somit die innere Reibung bestimmen (siehe auch
Kap.![]() 6.2.2).
6.2.2).
Die erzwungene Schwingung wird beschrieben durch die inhomogene Differentialgleichung
![]() stellt die Kraft dar, die auf die Masse
stellt die Kraft dar, die auf die Masse
![]() im
Abstand
im
Abstand ![]() von der Einspannung wirkt.
von der Einspannung wirkt.
Die Funktionen ![]() aus Gl.
aus Gl.![]() (5.26) sind orthogonal
(5.26) sind orthogonal
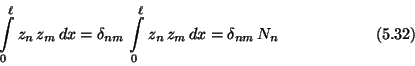
und zudem vollständig; daher läßt sich für beliebige Frequenzen
die Lösung der inhomogenen
Differentialgleichung (5.31) als Linearkombination der freien Eigenfunktionen
![]() darstellen. Es gilt somit /38/
darstellen. Es gilt somit /38/

mit
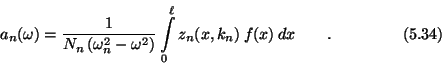
Im Falle einer nur am freien Ende des Plättchens angreifenden Kraft
vereinfacht sich (5.34) zu
so daß sich nun (5.33) schreiben läßt als
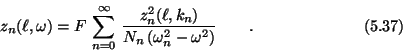
Bei Berücksichtigung der Dämpfung müssen wegen
![]() (Gl.
(Gl.![]() (5.23)) auch die Eigenfrequenzen komplex werden:
(5.23)) auch die Eigenfrequenzen komplex werden:
In der Nähe einer Resonanzstelle braucht in der Summe (5.37) nur der
dominierende Term berücksichtigt zu werden, so daß sich ergibt
Setzt man
![]() und
und
![]() , so erhält man für den relativen Betrag der Amplitude
, so erhält man für den relativen Betrag der Amplitude
also die vom gedämpften harmonischen Oszillator wohlbekannte Lorentzkurve.
Aus der Breite der Resonanzkurve läßt sich die innere Reibung bestimmen. Es
gilt nämlich
wobei ![]() den Frequenzabstand der beiden Punkte bezeichnet,
an denen die Amplitude auf
den Frequenzabstand der beiden Punkte bezeichnet,
an denen die Amplitude auf ![]() abgefallen ist (vgl.
abgefallen ist (vgl.![]() Kap. 6.2.2).
Kap. 6.2.2).
Auch die Phasenverschiebung zwischen erregender Kraft und Auslenkung verhält
sich genauso wie beim harmonischen Oszillator. Für den Phasenwinkel ![]() ergeben sich also die Beziehungen (s. auch Abb. 6.4)
ergeben sich also die Beziehungen (s. auch Abb. 6.4)
Der Frequenzgang der Amplitude läßt sich jedoch nicht nur in unmittelbarer
Umgebung einer Resonanzstelle, sondern für beliebige Frequenzen oder
Wellenzahlen bestimmen. Eine längere Rechnung ergibt nach /39/ den folgenden
Ausdruck für die komplexe Schwingungsamplitude am freien Ende:
wobei die komplexe Wellenzahl ![]() verwendet wurde:
verwendet wurde:
die für kleine Dämpfung (![]() ) genähert werden kann durch
) genähert werden kann durch
Abb. 5.5 zeigt den Betrag der komplexen Schwingungsamplitude bei ![]() als Funktion
des Realteils von
als Funktion
des Realteils von ![]() für zwei verschiedene Dämpfungswerte. Dabei wurde
angenommen, daß die Dämpfung frequenzunabhängig ist.
für zwei verschiedene Dämpfungswerte. Dabei wurde
angenommen, daß die Dämpfung frequenzunabhängig ist.
Die beiden Kurven sind praktisch nur in unmittelbarer Umgebung der Resonanzstellen unterscheidbar. Die tiefen Minima resultieren aus dem Wandern der Schwingungsknoten durch das Plättchenende.
Die Abhängigkeit der Resonanzfrequenz von der Dämpfung stimmt nicht mit der vom gedämpften harmonischen Oszillator bekannten überein. Während dort für die Frequenz des Amplitudenmaximums die Beziehung
gilt, liefert eine numerische Untersuchung der Lage der Amplitudenmaxima nach
Gl.![]() (5.44) ein komplizierteres Bild. Zwar ergibt sich auch hier
näherungsweise eine
quadratische Abhängigkeit von der inneren Reibung gemäß
(5.44) ein komplizierteres Bild. Zwar ergibt sich auch hier
näherungsweise eine
quadratische Abhängigkeit von der inneren Reibung gemäß
jedoch unterscheiden sich die Konstanten ![]() nach Vorzeichen und
Betrag voneinander. Man erhält
nach Vorzeichen und
Betrag voneinander. Man erhält
Abb. 5.6 illustriert dieses Verhalten.
Während die Resonanzfrequenz der Grundmode mit wachsender Dämpfung also zu
kleineren Werten verschoben wird, steigt die Frequenz der Obertöne bei Zunahme
der inneren Reibung an. Für Dämpfungen
![]() (wie in den
Experimenten der vorliegenden Arbeit) sind solche Korrekturen allerdings
ohnehin vernachlässigbar. Es sei jedoch darauf hingewiesen, daß
die hier gefundenen Ergebnisse nicht mit dem
Resultat aus /39/ übereinstimmen, wo
(wie in den
Experimenten der vorliegenden Arbeit) sind solche Korrekturen allerdings
ohnehin vernachlässigbar. Es sei jedoch darauf hingewiesen, daß
die hier gefundenen Ergebnisse nicht mit dem
Resultat aus /39/ übereinstimmen, wo
![]() ermittelt worden war.
ermittelt worden war.
In den vorausgehenden Abschnitten wurde das eingespannte Plättchen stets als
lineares System betrachtet. Dies führte zwangsläufig auf eine lineare
Bewegungsgleichung (Gln.![]() 5.14 bzw.
5.14 bzw.![]() 5.31), deren Lösungen dem
Superpositionsprinzip gehorchen und sich im Fall der erzwungenen Schwingung als
Linearkombination der freien Eigenmoden schreiben lassen. Man kann erwarten,
daß bei kleinen Auslenkungen des Reeds aus der Gleichgewichtslage -- und damit
kleinen Verzerrungen -- diese Beschreibungsweise eine gute Näherung darstellt.
Die dabei zugrundeliegende Theorie basiert auf der Annahme eines linearen
Zusammenhangs zwischen der Verzerrung
5.31), deren Lösungen dem
Superpositionsprinzip gehorchen und sich im Fall der erzwungenen Schwingung als
Linearkombination der freien Eigenmoden schreiben lassen. Man kann erwarten,
daß bei kleinen Auslenkungen des Reeds aus der Gleichgewichtslage -- und damit
kleinen Verzerrungen -- diese Beschreibungsweise eine gute Näherung darstellt.
Die dabei zugrundeliegende Theorie basiert auf der Annahme eines linearen
Zusammenhangs zwischen der Verzerrung ![]() und der mechanischen Spannung
und der mechanischen Spannung
![]() , wie etwa in Gl.
, wie etwa in Gl.![]() (5.1) (wobei diese Größen natürlich im allgemeinen
Tensorcharakter haben). Auch für den anelastischen Festkörper, bei dem also
Dämpfungseffekte eine Rolle spielen, ergibt sich ein linearer, wenngleich etwas
komplizierterer Zusammenhang zwischen
(5.1) (wobei diese Größen natürlich im allgemeinen
Tensorcharakter haben). Auch für den anelastischen Festkörper, bei dem also
Dämpfungseffekte eine Rolle spielen, ergibt sich ein linearer, wenngleich etwas
komplizierterer Zusammenhang zwischen ![]() und
und ![]() /40/, /41/:
/40/, /41/:
mit der Zeitverzögerung ![]() zwischen Spannungs- und Verzerrungsänderung und
den Elastizitätskonstanten
zwischen Spannungs- und Verzerrungsänderung und
den Elastizitätskonstanten ![]() , die sich mit dem Real- und Imaginärteil
eines komplexen Moduls, wie er etwa in Gl.
, die sich mit dem Real- und Imaginärteil
eines komplexen Moduls, wie er etwa in Gl.![]() (5.28) eingeführt wurde,
verknüpfen lassen.
(5.28) eingeführt wurde,
verknüpfen lassen.
Der Übergang zur nichtlinearen Beschreibungsweise erfolgt durch die Annahme,
daß die elastischen Konstanten selbst Funktionen der Verzerrung sind und sich
nach Potenzen von ![]() entwickeln lassen, wobei dann die
Entwicklungskoeffizienten die Elastizitätskonstanten höherer Ordnung
repräsentieren /42/. Im Grenzfall kleiner Verzerrungen ist nur der Term
0.
entwickeln lassen, wobei dann die
Entwicklungskoeffizienten die Elastizitätskonstanten höherer Ordnung
repräsentieren /42/. Im Grenzfall kleiner Verzerrungen ist nur der Term
0.![]() Ordnung von Bedeutung, so daß man (5.50) zurückerhält. Es existieren
verschiedene überlegungen, aus der Annahme eines solchen nichtlinearen
Verzerrungs-Spannungs-Zusammenhangs eine Bewegungsgleichung für das
Vibrating-Reed-System abzuleiten, die dann natürlich nicht mehr linear sein
wird /43/, /44/. Darauf soll hier im einzelnen nicht eingegangen werden, jedoch
seien einige bemerkenswerte Resultate, die sich teilweise auch aus Theorien für
andersartige nichtlineare Systeme ergeben, kurz skizziert.
Ordnung von Bedeutung, so daß man (5.50) zurückerhält. Es existieren
verschiedene überlegungen, aus der Annahme eines solchen nichtlinearen
Verzerrungs-Spannungs-Zusammenhangs eine Bewegungsgleichung für das
Vibrating-Reed-System abzuleiten, die dann natürlich nicht mehr linear sein
wird /43/, /44/. Darauf soll hier im einzelnen nicht eingegangen werden, jedoch
seien einige bemerkenswerte Resultate, die sich teilweise auch aus Theorien für
andersartige nichtlineare Systeme ergeben, kurz skizziert.
Schon die einfachsten nichtlinearen Bewegungsgleichungen wie z.B.![]() die des
anharmonischen Oszillators
die des
anharmonischen Oszillators
für den also die potentielle Energie bis zu Gliedern vierter Ordnung entwickelt
wurde, lassen sich nicht mehr exakt lösen. Allerdings kann man das Verfahren
der ,,sukzessiven Approximation`` anwenden, um wenigstens eine genäherte Lösung
einer nichtlinearen Bewegungsgleichung zu erhalten
(für Gl.
![]() /45/, /46/). Dabei ergibt sich u.a.
/45/, /46/). Dabei ergibt sich u.a.![]() das
Auftreten von Kombinationsfrequenzen, was etwa für den anharmonischen
Oszillator bedeutet, daß die Näherungslösung keine einfache periodische Form
hat, sondern neben einem Hauptanteil der Frequenz
das
Auftreten von Kombinationsfrequenzen, was etwa für den anharmonischen
Oszillator bedeutet, daß die Näherungslösung keine einfache periodische Form
hat, sondern neben einem Hauptanteil der Frequenz ![]() auch Terme der
Periodizität
auch Terme der
Periodizität ![]() enthält, wobei
enthält, wobei ![]() eine ganze Zahl ist. Die Amplituden
der Kombinationsschwingungen wachsen mit
eine ganze Zahl ist. Die Amplituden
der Kombinationsschwingungen wachsen mit ![]() an, wenn
an, wenn ![]() die Amplitude des
Terms der Frequenz
die Amplitude des
Terms der Frequenz ![]() ist; ihr relatives Gewicht nimmt also mit
größerwerdenden Auslenkungen zu.
ist; ihr relatives Gewicht nimmt also mit
größerwerdenden Auslenkungen zu.
Weiter zeigt sich, daß die Frequenz ![]() nicht mit der Eigenfrequenz
nicht mit der Eigenfrequenz
![]() des harmonischen Oszillators übereinstimmt, sondern eine (in zweiter
Näherung) mit
des harmonischen Oszillators übereinstimmt, sondern eine (in zweiter
Näherung) mit ![]() anwachsende Korrektur erfährt. Dabei hängen die Stärke und
die Richtung der Frequenzverschiebung vom Betrag und Vorzeichen der Parameter
anwachsende Korrektur erfährt. Dabei hängen die Stärke und
die Richtung der Frequenzverschiebung vom Betrag und Vorzeichen der Parameter
![]() und
und ![]() , bzw.
, bzw.![]() , allgemeiner gesprochen, vom Betrag
und Vorzeichen der elastischen Konstanten der verschiedenen Ordnungen ab. Der
Effekt läßt sich gut beobachten, wenn man das System in der Nähe einer
Resonanz zu erzwungenen Schwingungen anregt und die Frequenz der erregenden
Kraft allmählich variiert. Abb. 5.7 zeigt das qualitative Aussehen der dabei
entstehenden Resonanzkurven
, allgemeiner gesprochen, vom Betrag
und Vorzeichen der elastischen Konstanten der verschiedenen Ordnungen ab. Der
Effekt läßt sich gut beobachten, wenn man das System in der Nähe einer
Resonanz zu erzwungenen Schwingungen anregt und die Frequenz der erregenden
Kraft allmählich variiert. Abb. 5.7 zeigt das qualitative Aussehen der dabei
entstehenden Resonanzkurven ![]() für drei unterschiedliche Amplituden
der erregenden Kraft.
für drei unterschiedliche Amplituden
der erregenden Kraft.
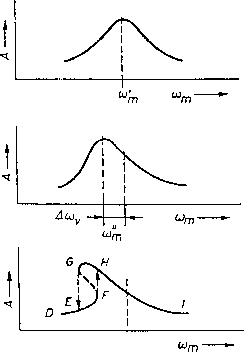
|
Abb. 5.7 Die Frequenzabhängigkeit der Schwingungsamplitude |
Bei kleinen Amplituden (oberes Bild) ergibt sich der harmonische Grenzfall, die Resonanzkurve hat die Lorentzform (5.40). Mit wachsender Anregung verschiebt sich das Amplitudenmaximum zu (in diesem Fall) niedrigeren Frequenzen, die Kurve wird asymmetrisch. Bei noch größerer erregender Kraft beobachtet man schließlich ein überkippen der Resonanzkurve, was zu Sprungphänomenen führt: Nähert man sich der Resonanzstelle von der niederfrequenten Seite, springt die Amplitude am Punkt F nach H, während man von hohen Frequenzen (Punkt I) herkommend den Sprung erst nach Durchlaufen des Punktes H von der Stelle G nach E beobachtet. Ein schönes Beispiel für das Auftreten dieser Sprungphänomene bei einem Vibrating-Reed-System zeigt Abb. 5.8:
Die Kurven kippen zunächst nach links (g), dann bei wachsender Amplitude nach rechts (f,e) und schließlich bei sehr großen Verzerrungen wieder nach links (d-a). Daraus lassen sich Rückschlüsse auf die Vorzeichen und Beträge der elastischen Konstanten höherer Ordnung ziehen /44/. In der gleichen Arbeit konnten außerdem die zugehörigen Resonanzkurven für die dritten Harmonischen (dreifache Frequenz der Grundschwingung) gemessen werden, deren Verzerungsamplituden bemerkenswert groß waren (für Kurve a etwa 40% der Verzerrung der Grundmode). Dies zeigt eindrucksvoll, daß bei großen Reedamplituden auch ganz andere Schwingungsformen als die für die lineare Theorie abgeleiteten Eigenmoden (5.26) existieren können.
Ein weiteres mögliches Merkmal anharmonischen Verhaltens ist die
Amplitudenabhängigkeit der Dämpfung. Die Auslenkung eines linearen Systems aus
seiner Gleichgewichtslage ist gerade proportional zu der Kraft, die es erfährt.
Der Quotient ![]() , der die Güte des Systems charakterisiert, ist also eine
einfache Konstante. Im nichtlinearen Fall dagegen gilt dieser simple
Zusammenhang nicht mehr notwendigerweise, die Schwingungsamplitude wächst dann
-- je nachdem -- schneller oder langsamer als die Amplitude der erregenden
Kraft. Eine einfache überprüfungsmöglichkeit dieses Verhaltens besteht in der
Beobachtung des Amplitudenzerfalls nach Aussschalten der Anregung. Auf einer
halblogarithmischen Skala müßte sich dann im linearen Fall (für das Reed gemäß
Gl. (5.29)) ein geradliniger Verlauf in der Zeitabhängigkeit der Amplitude
ergeben (s. z.B. Abb. 6.2).
Ist dagegen die Dämpfung amplitudenabhängig, beobachtet man eine
Krümmung des Graphen
, der die Güte des Systems charakterisiert, ist also eine
einfache Konstante. Im nichtlinearen Fall dagegen gilt dieser simple
Zusammenhang nicht mehr notwendigerweise, die Schwingungsamplitude wächst dann
-- je nachdem -- schneller oder langsamer als die Amplitude der erregenden
Kraft. Eine einfache überprüfungsmöglichkeit dieses Verhaltens besteht in der
Beobachtung des Amplitudenzerfalls nach Aussschalten der Anregung. Auf einer
halblogarithmischen Skala müßte sich dann im linearen Fall (für das Reed gemäß
Gl. (5.29)) ein geradliniger Verlauf in der Zeitabhängigkeit der Amplitude
ergeben (s. z.B. Abb. 6.2).
Ist dagegen die Dämpfung amplitudenabhängig, beobachtet man eine
Krümmung des Graphen ![]() (etwa wie in Abb. 8.3).
(etwa wie in Abb. 8.3).
Bei der Interpretation einer solchen
gekrümmten Kurve ist allerdings eine gewisse Vorsicht geboten, da die Krümmung
auch eine andere Ursache haben kann: Regt man das System nämlich nicht genau
mit der Resonanzfrequenz an, wird die resultierende Schwingung stets aus
mehreren Moden zusammengesetzt sein, zwischen denen sich nach Ausschalten der
äußeren Kraft Schwebungen herausbilden können. Dies führt natürlich ebenfalls
zu Abweichungen von der Linearität der
![]() -Kurve (s.
-Kurve (s.![]() z.B.
z.B.![]() /48/).
/48/).