diploma thesis J. Claßen

chapter 6

J. Claßen - Diplomarbeit

← Kapitel 5

6. Experimentelle Technik

6.1 Elektronischer Aufbau

Die in einem Vibrating-Reed-Experiment verwendeten Proben haben üblicherweise eine rechtwinklige Geometrie mit den typischen Dimensionen Länge $\ell \simeq 3 - 20\,$ mm, Breite $b \simeq 1 - 3\,$ mm und Dicke $d \simeq 0.03 - 0.3\,$ mm. Diese Plättchen werden an einem Ende zwischen zwei miteinander verschraubbare Klötzchen geklemmt, wobei in Tieftemperaturexperimenten aufgrund der erforderlichen hohen Wärmeleitfähigkeit im allgemeinen Kupfer als Probenhaltermaterial Verwendung findet.

Die Anregung des Plättchens zu erzwungenen Schwingungen erfolgt berührungsfrei auf elektrostatischem Wege. Falls das zu untersuchende Material nicht ohnenhin schon leitfähig ist (wie etwa im Falle metallischer Gläser), wird zunächst eine leitfähige Schicht auf die Probe gebracht, die natürlich so dünn gehalten werden muß, daß sie die elastischen Eigenschaften des Reeds nicht merklich beeinflußt. Bei den untersuchten Quarzglasproben wurde daher eine Goldschicht von wenigen Nanometern aufgesputtert.

Positioniert man nun auf Höhe des freien Endes des (über den Probenhalter geerdeten) Plättchens im Abstand $g_{\rm a}$ eine Elektrode, so bilden Reed und Elektrode einen Kondensator, zwischen dessen ,,Platten`` bei Anlegen einer Spannung die Kraft

$\begin{displaymath}F = {1 \over 2}\> C_{\rm a}\, {U^2 \over g_{\rm a}} \eqno (6.1) \end{displaymath}$

wirkt. Für $C_{\rm a}$ kann bei dem vorliegenden System näherungsweise die Kapazität eines Plattenkondensators der Grundfläche

$\begin{displaymath}C_{\rm a} = \epsilon_0\, {S\over g_{\rm a}} \eqno (6.2) \end{displaymath}$

angenommen werden. Bei Anlegen einer Wechselspannung

$\begin{displaymath}U(t) = U_0 \cos\left({1 \over 2}\> \omega t\right) \eqno (6.3) \end{displaymath}$

ergibt sich für die Zeitabhängigkeit der Kraft

$\begin{displaymath}F(t) = {1 \over 4}\> C_{\rm a}\>{U_0^2 \over g_{\rm a}}\> (1+\cos \omega t) \qquad .\eqno (6.4) \end{displaymath}$

Die Probe schwingt also mit der doppelten Frequenz der Anregungsspannung. Dabei ändert sich natürlich der Abstand $g_{\rm a}$ zwischen Elektrode und Probe, was über die in Kap. $\,$ 5.5 diskutierten Effekte hinaus zu nichtlinearem Verhalten führen kann. Falls dieser Effekt bei großen Schwingungsamplituden tatsächlich von Bedeutung sein sollte, müßte er sich leicht nachweisen lassen: Bei Durchfahren einer Resonanzkurve nähme die wirksame Kraft mit wachsender Amplitude stetig zu, was zu einer überhöhung der Resonanzspitze gegenüber der Lorentzform (5.40) (nicht aber zu einer Verkippung der gesamten Kurve $\,$ !) führen sollte. Im Rahmen dieser Arbeit wurde ein solches Verhalten nicht beobachtet; dies legt nahe, daß die Annahme einer auslenkungsunabhängigen Anregungskraft zulässig ist.

Zum Nachweis der Schwingungen macht man sich die Tatsache zunutze, daß eine Abstandsänderung zwischen den Elektroden eines Kondensators eine Kapazitätsänderung zur Folge hat. Man bringt eine weitere Elektrode auf der anderen Seite der Probe (der Anregungselektrode gegenüber) an, die nun ebenfalls einen Kondensator mit dem eingespannten Plättchen bildet. Dessen Kapazität ist gegeben durch

$\begin{displaymath}C = C_{\rm d}\> {1 \over 1-z/g_{\rm d}} \simeq C_{\rm d}\>(1+z/g_{\rm d}) \qquad , \eqno (6.5) \end{displaymath}$

wobei bei der letzten Näherung angenommen wurde, daß die Schwingungsamplitude wesentlich kleiner als der Gleichgewichtsabstand $g_{\rm d}$ zwischen Reed und Detektionselektrode ist. Für $C_{\rm d}$ gilt analog zu Gl. $\,$ (6.2) $C_{\rm d} = \epsilon_0 S/g_{\rm d}$ . Legt man über einen Widerstand eine Gleichspannung $U_{\rm B}$ an die Detektionselektrode an, so fällt aufgrund der Kapazitätsänderung durch die Reedschwingung über dem Widerstand eine Wechselspannung ab, die sich unter Berücksichtigung der Leitungskapazität $C_{\rm L}$ zu

$\begin{displaymath}U_{\rm d} = U_{\rm B} \, {z \over g_{\rm d}} \> {C_{\rm d} \... ...er \sqrt{1+(\omega R\> (C_{\rm d}+C_{\rm L}))^2}} \eqno (6.6) \end{displaymath}$

ergibt /49/. Typische Werte für die verwendeten Größen sind

$\begin{displaymath}\eqalignno { U_{\rm B} & \simeq 100\,{\rm V} & \cr g_{\rm d}... ...pF} & \cr R \>\, & \simeq 300\,{\rm M}\Omega \qquad . & \cr } \end{displaymath}$

Bei den im Experiment benutzten Meßfrequenzen $\omega /2\pi > 1 \, {\rm kHz}$ kann der letzte Faktor in Gl. $\,$ (6.6) in guter Näherung durch 1 ersetzt werden, so daß das übertragungsverhältnis $\vert U_{\rm d}/z \vert$ frequenzunabhängig wird. Schwingungsamplitude und Detektionsspannung sind dann zueinander proportional, und wegen $C_{\rm d} \ll C_{\rm L}$ kann man vereinfachend schreiben

$\begin{displaymath}U_{\rm d} \simeq U_{\rm B}\,{z \over g_{\rm d}} \> {C_{\rm d} \over C_{\rm L}} \qquad , \eqno (6.8) \end{displaymath}$

woraus man bei bekanntem $U_{\rm d}$ eine Abschätzung für die Schwingungsamplitude erhält. Einen schematischen überblick über den elektronischen Aufbau des gesamten Experimentes gibt Abb. $\,$ 6.1:

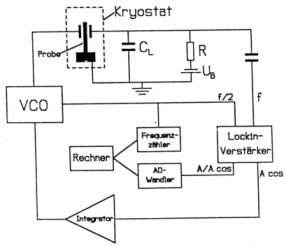
Abb. 6.1: Schematischer Aufbau der Meßelektronik für das Vibrating-Reed-Experiment.

Ein spannungsgesteuerter Oszillator (VCO), Wavetek 162, regt die Probe mit der Frequenz zu Schwingungen der Frequenz an. Die dadurch im Nachweiskreis erzeugte Wechselspannung wird von einem phasenempfindlichen Verstärker, Ithaco 393, (Lock-in-Verstärker) detektiert. Diesem Meßverstärker wird außerdem noch auf seinen Referenzeingang das Anregungssignal des VCO zugeführt. Da die Anregung nur die halbe Frequenz des Detektionssignals aufweist, muß der Lock-in im -Betrieb arbeiten. Dies hat den Vorteil, daß er gegen mögliches übersprechen der Anregespannung auf die Detektionsseite relativ unempfindlich wird. Der Vergleich der Phasenlage der beiden Eingangssignale ermöglicht eine Bestimmung der Phasendifferenz $\varphi$ zwischen Anregung und Detektion. An den Ausgängen des Lock-in stehen die drei Signale $A,A\cos \varphi$ und $A\sin \varphi$ zur Verfügung, wobei eine der Detektionsspannung und somit auch der Schwingungsamplitude proportionale Gleichspannung ist. Die $A\cos \varphi$ -Funktion (Gl. $\,$ (5.42)) hat gerade bei der Resonanzfrequenz einen Nulldurchgang und eignet sich daher als Steuersignal zum Nachregeln der Anregefrequenz bei änderungen der Resonanzfrequenz. Dazu wird das $A\cos \varphi$ -Signal am Ausgang des Lock-in-Verstärkers über einen Integrator auf den Eingang des VCO gegeben. Im Falle $\omega < \omega_{\rm res}$ ist das $A\cos \varphi$ -Signal positiv; über den Integrator wird dann eine Spannung an den VCO geliefert, die eine Erhöhung der Anregefrequenz bewirkt. Für $\omega > \omega_{\rm res}$ kehren sich die Vorzeichen um, so daß die Frequenz des VCO erniedrigt wird. Damit ist ein Regelkreis aufgebaut, der das schwingende Plättchen automatisch in Resonanz hält. (Bei dem in den Experimenten dieser Arbeit verwendeten Intgrator bewirkte ein positives $A\cos \varphi$ -Signal eine Verminderung der Anregungsfrequenz des VCO. Daher wurde dem Signal eine zusätzliche Phasenverschiebung von $\pi$ aufgeprägt, was gerade einer Vorzeichenumkehr des $\cos \varphi$ entspricht, vgl. $\,$ Abb. $\,$ 6.4.) Von einem Personal Computer wurden über einen Frequenzzähler die Frequenz des VCO und über einen A/D-Wandler das Ausgangssignal des Lock-in-Verstärkers eingelesen und mit Hilfe eines Meßprogramms ausgewertet.

6.2 Bestimmung der Meßgrößen

6.2.1 Relative Änderung der Schallgeschwindigkeit

Wie man an Gl. $\,$ (5.23) erkennt, erfordert die Bestimmung der absoluten Schallgeschwindigkeit $v_{\rm Y}$ aus den gemessenen Resonanzfrequenzen eine genaue Kenntnis der Probengeometrie. Doch selbst bei präziser Ausmessung der Reedlänge und -dicke -- was ohnehin immer noch Fehler von einigen Prozent einschließt -- ist nicht unbedingt mit korrekten Absolutwerten der Schallgeschwindigkeit zu rechnen, da in Gl. $\,$ (5.23) einige Näherungen und Idealisierungen eingingen (exakt rechteckiger Querschnitt und homogene Dicke der Probe, Breite wesentlich kleiner als Länge), die im Experiment sicherlich nur unzureichend realisiert sind. Jedoch lassen sich, sofern die thermische Expansion vernachlässigbar ist -- was bei tiefen Temperaturen ( $T<1\,\rm K$ ) für praktisch alle Substanzen und für Quarzglas in guter Näherung auch im gesamten vermessenen Temperaturbereich gewährleistet ist (der Expansionkoeffizient von Quarzglas beträgt nach /50/ bei 300 $\,$ K weniger als $6 \times 10^{-7}\,\rm K^{-1}$ ) -- relative änderungen der Schallgeschwindigkeit sehr genau vermessen, da sich ja unter den obigen Voraussetzungen $f_n = {\rm const} \times v_{\rm Y}$ und somit

$\begin{displaymath}{\Delta\! f_n \over f_n} = {\Delta v_{\rm Y} \over v_{\rm Y}} \eqno (6.9) \end{displaymath}$

mit

$\begin{displaymath}{\Delta\! f_n \over f_n} = {f_n(T)-f_n(T_0) \over f_n(T_0)} \eqno (6.10) \end{displaymath}$

sowie dem entsprechenden Ausdruck für die Schallgeschwindigkeit ergibt. Hält man das Reed mit Hilfe der im vorigen Abschnitt beschriebenen Regelschleife in Resonanz, ergibt sich aus der Verschiebung der Resonanzfrequenz mit der Temperatur also direkt der Temperaturgang der Schallgeschwindigkeit. Die Genauigkeit der Frequenzmessung liegt typischerweise zwischen einigen $10^{-7}$ und etwa $10^{-5}$ , je nach Stabilität der Meßelektronik, Temperaturstabilität und Qualität des detektierten Signals.

6.2.2 Innere Reibung

Die einfachste Methode zur Bestimmung der inneren Reibung ergibt sich aus der Beobachtung des freien Amplitudenzerfalls. Regt man das Reed auf seiner Resonanzfrequenz zu erzwungenen Schwingungen an und schaltet dann die erregende Kraft aus, beobachtet man das mit der Zeit exponentielle Abklingen der Amplitude $A(t) = A_0\, e^{-t/\tau}$ , woraus sich mit Hilfe von $Q^{-1} = 1/\pi f_n \tau$ (Gl. $\,$ (5.30)) sofort der Wert der inneren Reibung ergibt. Diese Methode ist recht unkompliziert und ermöglicht vor allem auch eine sehr rasche Bestimmung von $Q^{-1}$ . Typische Fehlerschranken liegen im Bereich zwischen etwa 1 und 5%. Abb. $\,$ 6.2 zeigt ein Beispiel einer Zerfallskurve. In der Abbildung erkennt man auch den Amplitudenanstieg gemäß

$\begin{displaymath}A(t) = A_0\> (1 - e^{-t/\tau}) \qquad , \eqno (6.11) \end{displaymath}$

aus dem man prinzipiell ebenfalls die Zeitkonstante $\tau$ und damit die innere Reibung ablesen kann. Gl. $\,$ (6.11) ist allerdings nur erfüllt, wenn die Anregungsfrequenz mit der Resonanzfrequenz des Reeds übereinstimmt.

Abb. 6.2: Exponentieller Zerfall der Schwingungsamplitude. Bei $t = 1.5\,{\rm s}$ wurde die anregende Kraft ausgeschaltet, bei $t = 11\,{\rm s}$ wieder eingeschaltet usw.

Im Falle einer Differenz $\Delta\! f = f - f_{\rm res}$ zwischen Anregungs- und Eigenfrequenz beobachtet man eine überlagerung der exponentiellen Amplitudenzunahme mit einem exponentiell gedämpften Schwebungssignal der Frequenz $\Delta\! f$ . Der Amplitudenverlauf gehorcht dabei der Beziehung /51/

$\begin{displaymath}A(t) = A_0 \> \sqrt { 1 + e^{-t/\tau} - 2e^{-t/2\tau} \cos\,(2\pi (f-f_{\rm res})\,t)}\qquad ,\eqno (6.12) \end{displaymath}$

mit deren Hilfe man unter Benutzung eines Fitprogramms die gesuchten Parameter $f_{\rm res}$ und $Q^{-1}$ ermitteln kann. Diese Methode ist allerdings vergleichsweise ungenau und wurde nur zu Testzwecken verwendet. Abb. $\,$ 6.3 zeigt den zeitlichen Verlauf eines typischen Einschwingvorgangs.

Die bisher skizzierten Methoden zur Bestimmung der inneren Reibung sind allerdings nur dann anwendbar, wenn die Zeitkonstante $\tau$ des Aus- oder Einschwingvorgangs genügend groß ist. Erfolgt der Amplitudenzerfall schneller als binnen etwa 1 $\,$ s, kann er mit der im Experiment verwendeten Elektronik nicht mehr hinreichend aufgelöst werden. Bei einer typischen Vibrating-Reed-Meßfrequenz von etwa 1 $\,$ kHz bedeutet die Bedingung $\tau > 1\,$ s also, daß die innere Reibung kleiner als wenige $10^{-4}$ sein muß, bei höheren Frequenzen entsprechend noch niedriger.

Abb. 6.3: Einschwingverhalten des Reeds bei Anregung mit einer von der Eigenfrequenz abweichenden Frequenz. Die auftretende Schwebung ist exponentiell gedämpft und daher bereits nach wenigen Sekunden nicht mehr sichtbar. Die durchgezogene Linie entspricht (bis auf eine Verschiebung des Zeitnullpunktes) einem Fit nach Gl. $\,$ (6.12).

Im Falle großer Dämpfung und/oder hoher Frequenz wird die innere Reibung besser durch Aufnehmem von Resonanzkurven bestimmt, wobei für die Frequenzabhängigkeit der drei zur Verfügung stehenden Signale $A,A\cos \varphi$ und $A\sin \varphi$ die durch die Gln. $\,$ (5.40), (5.42), (5.43) gegebenen Ausdrücke gelten. Abb. $\,$ 6.4 zeigt das Resonanzverhalten des Reeds.

Abb. 6.3: Die Resonanzkurven

, $A\cos(\varphi+\pi)$ , $A\sin \varphi$ . Die Addition des Phasenfaktors $\pi$ entspricht einer Multiplikation der Kosinuskurve mit -1
(s. $\>$ Abschnitt 6.1). Die durchgezogenen Linien sind Fits nach den Gln. $\,$ (5.40),
(5.42), (5.43).

Aus der Breite der Kurven läßt sich gemäß $Q^{-1} =2\,\delta\!f/f_{\rm res}$ (Gl. $\,$ (5.41)) die innere Reibung bestimmen. Während für das reine Amplitudensignal $2\,\delta\!f$ durch den Frequenzabstand der Punkte gegeben ist, an denen die Amplitude vom Maximum auf den Wert $A_{\rm max}/\sqrt{2}$ abgefallen ist, sind die entsprechenden Punkte für die $A\sin \varphi$ -Kurve durch die Stellen, wo $A = A_{\rm max}/2$ gilt, und für das $A\cos \varphi$ -Signal durch die Frequenzlage der beiden Extrema gekennzeichnet (s. $\,$ Abb. $\,$ 6.4). Auch bei der Aufnahme von Resonanzkurven liegen die typischen Fehlerschranken bei der $Q^{-1}$ -Bestimmung im Bereich von 1-5% (s. $\>$ auch Kap. $\,$ 7.1).

Zu einer genaueren Bestimmung nicht des Absolutwertes, aber wenigstens des relativen Verlaufs der inneren Reibung eignet sich die Beziehung

$\begin{displaymath}Q \propto A\>f_{\rm res}^2 \qquad , \eqno (6.13) \end{displaymath}$

die aus Gl. $\,$ (5.39) für $f = f_{\rm res}$ folgt. Damit lassen sich noch änderungen von $Q^{-1}$ im Promillebereich auflösen. Im allgemeinen geht man daher so vor, daß man nur an ausgewählten Temperaturpunkten den Absolutwert der inneren Reibung durch Aufnahme von Resonanzkurven und/oder des Amplitudenzerfalls bestimmt und ansonsten lediglich die Amplitude und die Resonanzfrequenz $f_{\rm res}$ mißt, um daraus mit Hilfe von Gl. $\,$ (6.13) das jeweilige $Q^{-1}$ zu errechnen.

6.2.3 Mögliche Fehlerquellen

Bei einem Vibrating-Reed-Experiment gibt es verschiedene systematische Fehlerquellen, die die Meßergebnisse mehr oder minder stark verfälschen können. Einige davon spielen für die in dieser Arbeit durchgeführten Experimente jedoch keine nennenswerte Rolle, wie man sich anhand der in /49/ angegebenen Abschätzungen leicht überlegen kann, und seien daher nur stichwortartig erwähnt: -- Restgasdämpfung: Die Viskosität der umgebenden Atmosphäre führt zu einer Dämpfung der Probenschwingung. Für die im Experiment gebräuchlichen niedrigen Drücke $p < 10^{-5}\,$ mbar kann dieser Effekt vernachlässigt werden. -- Dämpfung durch Wärmeleitung der Probe: Während des Schwingungsvorgangs werden die Seiten des Reeds abwechselnd gedehnt und gestaucht, womit eine Temperaturerniedrigung bzw. -erhöhung einhergeht. Falls die Zeitkonstante $\tau$ des resultierenden Wärmeaustauschs vergleichbar mit der inversen Schwingungsfrequenz ist ( $\omega \tau \simeq 1$ ), wird der Schwingung Energie entzogen. Die sich ergebenden Verluste sind jedoch für die Experimente dieser Arbeit wiederum verschwindend gering. -- Elektromechanische Wandlerverluste: Durch die Probenschwingung wird auf der Detektionsseite am Widerstand eine elektrische Wechselspannung erzeugt (Gl. (6.6)). Die dazu erforderliche Leistung, die natürlich der Schwingung entzogen wird, entspricht aber nur einem gänzlich unbedeutenden Bruchteil der gesamten Schwingungsenergie, so daß auch dieser Effekt nicht von Bedeutung ist.

Schwieriger zu beurteilen ist der Einfluß der Einspannung auf das Dämpfungsverhalten des Reeds. Es hat sich gezeigt, daß der genauen Geometrie der Einspannungsstelle besondere Bedeutung zukommt; dies ist auch nicht verwunderlich, da dort für alle Schwingungsmoden die maximale Verzerrung auftritt (s. $\,$ Abb. $\,$ 5.4). Somit besteht sicherlich eine besondere Anfälligkeit für mögliche Verluste durch mechanisch nicht ganz optimalen Kontakt zwischen Probe und Halterung. Als günstigste Form für die Kupferklötzchen, zwischen die das Reed geklemmt wird, hat sich eine streng rechtwinklige Geometrie ohne Fase (und natürlich auch ohne überstehende Grate, die oft aus dem Herstellungsprozeß resultieren) erwiesen. Die mikroskopischen Eigenschaften der Einspannung ändern sich vermutlich auch noch während eines Experimentes (etwa durch Variation der Temperatur), was oft als Ursache für starke Streuung oder unzureichende Reproduzierbarkeit von Meßergebnissen herangezogen wird. Dennoch wird der Beitrag der Einspannungsdämpfung für einzelne Meßreihen meist als konstant angenommen. über die Qualität dieser Näherung läßt sich nur schwerlich eine zuverlässige Aussage treffen. Mit dem in dieser Arbeit größtenteils verwendeten Probenhalter konnte immerhin der für ein Vibrating-Reed-Experiment recht niedrige Wert der inneren Reibung von etwa $2 \times 10^{-5}$ gemessen werden; dieser Wert wäre vermutlich noch unterschritten worden, wenn der zugängliche Meßbereich zu tieferen Temperaturen ( $T < 10\,$ mK) hätte erweitert werden können, da dort die intrinsische Probendämpfung weiter abnimmt. Die Vermutung liegt also nahe, daß die Einspannungsdämpfung über einen sehr großen Teil des untersuchten Temperaturbereichs (wo die typischen Dämpfungswerte bei einigen $10^{-4}$ lagen) nur einen vergleichsweise geringen Einfluß hat und die gemessenen Absolutwerte der inneren Reibung tatsächlich im wesentlichen die intrinsische Dämpfung des Probenmaterials charakterisieren.

Ein weiteres Problem ergibt sich aus der bei der Schwingung der Probe dissipierten Leistung. Während bei Temperaturen bis hinab zu einigen hundert mK das thermische Gleichgewicht durch diesen Heizeffekt sicherlich nicht maßgeblich gestört wird, muß er bei tiefen Temperaturen, wo Wärmeleitung und Wärmekapazität von Probe und Halterung schnell abnehmen, unter Umständen berücksichtigt werden. Für die dissipierte Leistung kann man schreiben:

$\begin{displaymath}P = \pi^3 m\, Q^{-1} z^2 f^3 \qquad , \eqno (6.14) \end{displaymath}$

wobei die Masse der Probe bezeichnet. (Bei fest vorgegebener anregender Kraft bedeutet Gl. $\,$ (6.14) bemerkenswerterweise, daß die erzeugte Wärme mit abnehmender Dämpfung zunimmt, da ja die Schwingungsamplitude proportional zu ist.) Um berechnen zu können, muß die Schwingungsamplitude bekannt sein. Sie läßt sich sowohl von der Detektionsseite -- durch die über dem Widerstand abfallende Wechselspannung (Gl. $\,$ (6.8)) -- als auch von der Anregungsseite -- durch die auf das Reed wirkende elektrostatische Kraft -- abschätzen. Für die Anregungsseite gilt die Beziehung

$\begin{displaymath}z = {F \over \pi^2 m\, Q^{-1} f^2} = {C_{\rm a}\, U_0^{\,2} \over 4 \pi^2 g_{\rm a}\, m\, Q^{-1} f^2} \eqno (6.15) \end{displaymath}$

mit den im Abschnitt 6.1 eingeführten Bezeichnungen. Die dissipierte Leistung hängt also empfindlich von der Anregungsspannung ab ( $P \propto U_0^{\,4}\,$ ); daher darf , sollen Heizungseffekte vermieden werden, nicht zu groß gewählt werden. Der tatsächliche Einfluß der Probenheizung wird bei der Betrachtung der Meßergebnisse an $\rm Pd_{30} Zr_{70}$ in Kap. $\,$ 8 eingehender untersucht.

6.3 Erzeugung tiefer Temperaturen -- Der Kryostat

Flüssigkeiten lassen sich durch Abpumpen der umgebenden Atmosphäre kühlen. Erniedrigt man nämlich den Druck unter den Dampfdruck der Flüssigkeit, so treten Teilchen von der flüssigen in die gasförmige Phase über, in der sie eine wesentlich größere Entropie haben. Der Flüssigkeit wird dabei die Wärmemenge $dQ = T\,dS$ entzogen, wenn den Entropiezuwachs der Teilchen beim übergang in den neuen Aggregatzustand bezeichnet. Mit He können auf diese Weise Temperaturen von etwa 1 $\,$ K, mit He sogar 0.3 $\,$ K erreicht werden. Um noch tiefere Temperaturen zu erzeugen, muß man andere Kühlverfahren anwenden.

Die Experimente dieser Arbeit wurden in zwei He/He-Verdünnungskryostaten durchgeführt, bei denen die erreichten Minimaltemperaturen bei etwa 10 bzw. $\>$ knapp 40 $\,$ mK lagen. Das Funktionsprinzip dieser Kryostaten beruht auf den Eigenschaften von flüssigen He/He-Mischungen. Kühlt man ein solches Gemisch auf Temperaturen unterhalb von 0.8 $\,$ K ab, kann eine Phasentrennung zwischen einer fast ausschließlich aus He-Atomen und einer schwereren Schicht aus einer Mischung von He- und He-Atomen erfolgen. Der Anteil von He-Atomen in der He-reichen Phase ist temperaturabhängig und geht für $T \to 0$ auf ca. $\,$ 6% zurück.

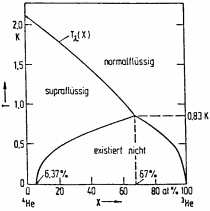
Abb. 6.5: Das Phasendiagramm von flüssigen

He/

He-Mischungen. X bezeichnet den prozentualen Anteil der

He-Atome an der Gesamtteilchenzahl. Die Temperatur der Phasentrennung ist konzentrationsabhängig.

Die He-Komponente in der schwereren Schicht ist suprafluid und trägt daher kaum zur Entropie bei. Aufgrund der Suprafluidität wechselwirken auch die He-Atome innerhalb dieser Phase kaum mit den He-Atomen und verhalten sich folglich beinahe wie Gasatome im Vakuum. Da die Dichte der He-Teilchen und damit ihre Wechselwirkung untereinander in der He-armen Phase geringer ist, haben sie eine deutlich höhere Entropie als die Atome in der He-reichen Schicht. Tritt nun ein Teilchen von der He-reichen in die He-arme Schicht über, ist damit wie beim eingangs erwähnten Verdampfungsprozeß eine Kühlung verbunden. (Man spricht daher auch von ,,Quasiverdampfung``.)

Die Nutzbarmachung dieses Kühlprinzips für einen kontinuierlichen Betrieb erfordert den Aufbau eines Kreislaufs, bei dem das He aus der schweren Phase abgeführt und in die leichte Phase nachgeliefert werden kann. In einem He/He-Verdünnungskryostaten (Abb. $\,$ 6.6) wird dies folgendermaßen realisiert: Die wesentlichen Teile der Apparatur befinden sich in einem Vakuumbehälter, der von flüssigem He ( $T \simeq 4.2\,$ K)

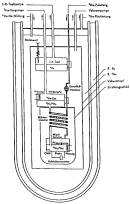
Abb. 6.6: Schematischer Aufbau eines

He/

He-Verdünnungskryostaten.

umgeben ist. über ein Nadelventil wird der 1 $\,$ K-Topf mit flüssigem He aus diesem Bad gefüllt. Durch Abpumpen des flüssigen Heliums wird seine Temperatur auf etwa 1.2 $\,$ K reduziert. Eine thermische Ankopplung der Zuleitung für das He/He-Gemisch am 1 $\,$ K-Topf bewirkt, daß dieses beim Vorbeiströmen kondensiert. Die nachgeschaltete Durchflußimpedanz gewährleistet dabei die Aufrechterhaltung des notwendigen Einkondensierdrucks. Nach einer Abkühlung des Gemisches auf 600-700 $\,$ mK durch eine thermische Ankopplung am Verdampfer gelangt es in ein System von Wärmetauschern, in denen aus der Mischkammer aufsteigendes kaltes He (s. $\,$ weiter unten) eine weitere allmähliche Reduktion der Temperatur der hinunterströmenden Flüssigkeit bewirkt. (Die Qualität der Wärmetauscher ist von entscheidender Bedeutung für die Effizienz des gesamten Kühlprozesses. Aus der unterschiedlichen Konstruktion der Wärmetauscher erklären sich auch die beträchtlichen Unterschiede in den Endtemperaturen der beiden verwendeten Kryostaten.) Schließlich erreicht das Gemisch die He-reiche Phase in der Mischkammer, wo der oben beschriebene Kühlprozeß erfolgt. Der erforderliche übertritt der He-Atome in die untere He-arme Schicht wird durch ein Konzentrationsgefälle an He-Teilchen zwischen den Gemischen im Verdampfer und im unteren Mischkammerbereich hervorgerufen. Am Verdampfer wird nämlich das He/He-Gemisch gepumpt, wobei fast nur He-Teilchen abdampfen, da bei (den mit Hilfe einer Heizung eingestellten) Temperaturen von 600-700 $\,$ mK der Dampfdruck von He etwa zwei Größenordnungen höher als der von He ist. (Im stationären Betrieb zirkulieren daher fast nur He-Atome.) Das resultierende Konzentrationsgefälle erzeugt einen osmotischen Druck, der für das Nachfließen von He aus der unteren Phase der Mischkammer zum Verdampfer sorgt. Da aber die Konzentration von He in der He-armen Schicht -- der jeweiligen Temperatur entsprechend -- konstant bleiben muß, ist dies nur möglich, wenn Teilchen aus der oberen Schicht in die untere übertreten und dabei ihre Umgebung abkühlen.

Zur Bestimmung der am Probenhalter vorliegenden Temperatur standen verschiedene Widerstandsthermometer zur Verfügung. Die Messung des elektrischen Widerstandes erfolgte mit der sogenannten Vierdrahtmethode, die eine Vernachlässigung der Zuleitungswiderstände ermöglicht. Bei relativ hohen Temperaturen (40-300 $\,$ K) wurde ein Platinthermometer Pt $\,$ 100, bei mittleren (0.5-40 $\,$ K) ein Germanium- und bei den tiefsten Temperaturen ein Kohlethermometer verwendet, dessen Eichbereich sich allerdings nur bis hinab zu 20 $\,$ mK erstreckte. Für tiefere Temperaturen mußten die Widerstandswerte mit Hilfe eines Polynomfits extrapoliert werden. Der Fehler dieses Verfahrens sollte nicht mehr als 10% betragen, ist damit aber deutlich größer als der Fehler im Gültigkeitsbereich der Eichtabellen, der bei etwa 1-3% liegen dürfte.

← Kapitel 5

KIP user name
Password

Information about the Login